Matrix Arrangement for Cat Sheet 5
- Jul 10
- 6 min read

Practicse Question
Matrix Arrangement CAT Case 1
Directions for questions 1 to 4 : Answer the questions on the basis of the information given below.In the (3 × 3) grid given below the Natural numbers from 1 to 9 are to be filled, one in each box.
Note: The rows are counted from top to bottom and the columns are counted from left to right.(i) The number in the box in first row and first column is 1 and the number in the box in second row and second column is 5.(ii) The sum of the 3 numbers in the first row is a prime number and the same is also true for the sum of the 3 numbers in the third row. Further, the sum of the 3 numbers in the first row is less than the sum of the 3 numbers in the third row.(iii) The sum of the 3 numbers in the second row is the average of the sum of the 3 numbers in the first row and the sum of the 3 numbers in the third row.(iv) For each row, the number in the first column is less than the number in the 2nd column, which is less than the number in the third column.
Q.1 How many different values of the number in the box in first row and third column are possible?
a.3
b.4
c.5
d.6
Q.2 If the number in the box in first row and third column is highest possible, what could be the value of the smallest number in third row and first column?
Q.3 What could be the maximum value of the sum of the 3 numbers in the diagonally present 3 boxes?
a.Given that the 3 boxes present diagonally are:
b.(a) box in the 1st row and 1st column, box in 2nd row and 2nd column and box in 3rd row and 3rd column;
c.OR
d.(b) box in 1st row and 3rd column, box in 2nd row and 2nd column and box in 3rd row and 1st column.
Q.4 What is the sum of all the distinct numbers possible in the box in third row and second column?
a.18
b.21
c.24
d.20
Matrix Arragement for CAT Case 2
Directions for questions 5 to 8: Answer the questions on the basis of the information given below.A shopkeeper has items of type A, type B, type C, and so on. He has several items of each type. The shopkeeper also has a 3 × 3 square matrix grid. He places exactly one item in each of the cell of the grid. He places the items in a particular manner. He chooses a cell and places a type A item in it, then he places a type B item in each of the cell adjacent to the one containing the type A item, then he places a type C item in each of the cells adjacent to the ones containing a type B item..... and so on. Two cells are called adjacent if they touch each other horizontally or vertically. Cells that touch each other diagonally do not count as adjacent. Consider the cells of the grid are distinctly numbered.
Q.5 In how many cells, is it possible to place a type E item?
Q.6 Suppose the shopkeeper also has a 5 × 5 square matrix grid. And he places the items in the cells of the grid in the same manner. Consider the cells of this grid are also distinctly numbered. What is the maximum number of distinct types of items that can be placed in this grid?
Q.7 Suppose the shopkeeper also has a 5 × 5 square matrix grid. And he places the items in the cells of the grid in the same manner. Consider the cells of this grid are also distinctly numbered. In how many of the cells can the type A item be placed, so that this grid contains exactly seven distinct types of items?
Q.8 Taking a 3 × 3 square matrix grid, the shopkeeper now chooses a pair of cells instead, and places a type A item in each. He then places the items in the cells of this grid in the same manner: he places a type B item in each of the cells adjacent to the ones containing a type A item, then he places a type C item in each of the cells adjacent to the ones containing a type B item..... and so on. How many different grids are possible by placing a type D item in such a grid?
a.16
b.14
c.18
d.12
Matrix Arrangement for CAT Case 3
Refer to the data below and answer the questions that follow.Four farmers F1, F2, F3 and F4 own Mango Bagaans in six villages viz. Velas, Vadavali, Gondghar, Kurang, Kudgaon and Dabhol. Each farmer owns at least one Bagaan in each of the villages. The maximum number of Bagaans owned by any farmer in any village is 24. The number of Bagaans owned by each farmer in each village is a distinct integer.
The following points are known:1. The total number of Mango Bagaans owned by each of F4, F3, F2 and F1 form an Arithmetic Progression in that order with common difference = 2.2. The sum of the Mango Bagaans owned by the four farmers in each of Vadavali, Gondghar and Kurang is equal.3. The sum of the Mango Bagaans owned by the four farmers in Velas, Kudgaon and Dabhol are consecutive integers in some order.
The following table gives the partial information about the Bagaans owned by four farmers in six villages:
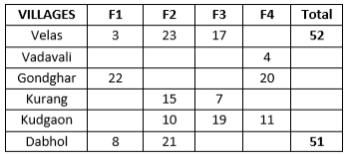
Q.9 Find the total number of Bagaans owned by all four farmers in Kudgaon.
Q.10 Who owns the maximum number of Bagaans in any of the six villages?
a.F1
b.F2
c.F3
d.F4
Q.11 How many Bagaans does F1 own in Kurang?
a.12
b.13
c.14
d.16
Q.12 What is the difference between the number of Bagaans owned by F2 in Vadavali and Gondghar?
a.2
b.3
c.4
d.5
Q.13 How many Bagaans does F3 own in Dabhol?
a.1
b.5
c.6
d.10
Matrix Arrangement for CAT Case 4
Refer to the data below and answer the questions that follow.The British Philosophy Association (BPA) invited the opinions of scholars on the most influential Philosopher in the history of Europe. The scholars were divided into four groups depending on the number of years of research experience: 1 to 5 years, 6 to 10 years, 11 to 15 years and more than 15 years. Together there were 500 scholars in all in these four groups. The five philosophers, namely Locke, Mill, Smith, Ricardo and Spencer were the top five philosophers voted by each of the four groups. Each scholar voted for exactly one philosopher.
The following table shows the number of scholars in the four groups who voted for these five philosophers. These five philosophers have been disguised as ‘A’, ’B’, ’C’, ’D’ and ‘E’.

Additionally, the following points are known:
1. Spencer and Locke received equal numbers of votes in exactly one group. Similarly, Ricardo and Smith received equal numbers of votes in exactly one group. Similarly, the following two pairs: Mill and Ricardo & Mill and Smith also received equal numbers of votes in exactly one group.
2. Mill received more votes than Spencer did in exactly three groups out of the four.
3. Smith received more votes than Ricardo did in only one group out of the four.
Q.14 For how many Philosophers, can we uniquely determine the disguises used for them?
Q.15 How many votes did Smith receive in the group ‘More than 15 years’? (Write 0 if your answer is ‘Cannot be determined’).
Q.16 Which of the following statements is incorrect?
a.Smith received more votes than Mill in exactly two groups out of the four.
b.Spencer received more votes than Ricardo in only one group out of the four.
c.Ricardo received more votes than Locke in only one group out of the four.
d. Locke received more votes than Mill in exactly two groups out of the four.
Q.17 In which of the following groups did Mill receive the highest number of votes?
a.More than 15 years
b.11 to 15 years
c.6 to 10 years
d.1 to 5 years
Q.18 What is the ratio of the number of votes received by Mill in the '6 to 10 years' group to the number of votes received by Smith in the 'More than 15 years' group?
a.1 : 1
b.1 : 4
c.2 : 1
d.4 : 1




Comments